Come già indicato nella pagina del "Sudoku 9x9 Logic Solver & Report Builder", chi vuole maggiori informazioni su "Alternating Inference Chains" (Forbidding Chains) può visitare il sito di Bruno Greco (dove sono spiegati benissimo i concetti base delle catene: veramente ottimo per "absolute beginners"), oppure il blog di sudoku.com.au (molti esempi e discussioni su catene di tutti i tipi: di questo blog meglio visitare prima le pagine meno recenti per chi sta iniziando ad utilizzare questa tecnica).
Sintetizzando il vastissimo argomento, le regole base sono:
- si definisce un'inferenza forte (strong link / thick link) fra due candidati quando almeno uno dei due è vero → in pratica quando i due candidati sono soli e uguali all'interno di una riga/colonna/riquadro o sono i soli all'interno della stessa cella (vale anche tra un candidato singolo e un gruppo di altri candidati o fra due gruppi): almeno uno diventa ovviamente solo uno in un'inferenza forte diretta fra due candidati, ma possono essere veri tutti e due in un'inferenza forte fra due vertici di una catena di cui al punto 3
- si definisce un'inferenza debole (weak link / thin link) fra due candidati quando al massimo uno dei due è vero (potrebbero essere falsi tutti e due ma non veri tutti e due) → in pratica quando i due candidati non sono i soli ma sono uguali all'interno di una riga/colonna/riquadro o non sono i soli all'interno della stessa cella (vale anche tra un candidato singolo e un gruppo di altri candidati o fra più gruppi)
- in una "Alternating Inference Chain" (Forbidding Chain) composta alternativamente da un'inferenza forte e una debole (con un'inferenza forte iniziale e finale) i due candidati (o gruppi) disposti ai vertici (inizio e fine) della catena sono anch'essi legati da un'inferenza forte (quindi almeno uno dei due è vero) → per la dimostrazione vedi i link consigliati sopra
- nella composizione di una "Alternating Inference Chain" (Forbidding
Chain) quindi:
- iniziamo con una coppia di candidati (o candidato + blocco) legati con un'inferenza forte
- colleghiamo poi un altro elemento con inferenza debole → se non esiste possiamo sostituirlo con uno che potrebbe essere collegato con una seconda inferenza forte consecutiva ma considerandolo comunque un weak link
- aggiungiamo un ulteriore elemento collegabile in inferenza forte e valutiamo gli altri candidati dello schema secondo i parametri dei punti 5 e 6
- proseguiamo eventualmente aggiungendo alla catena altre coppie di inferenze deboli + forti e ripetiamo le valutazioni finché riusciamo a trovare altre inferenze
- se possiamo sostituire un'inferenza debole con una forte (ma considerandola comunque debole) non possiamo fare il contrario sostituendo un'inferenza forte con una debole
- una "Alternating Inference Chain" (Forbidding Chain) valida è composta sempre da un numero pari di elementi (candidati singoli o blocchi) legati da un numero dispari di inferenze alternate forti/deboli di cui la prima e l'ultima sono forti (salvo il caso delle catene circolari bidirezionali di cui al punto 6)
- ogni candidato che nello schema "vede" (o meglio è collegabile con un'inferenza debole a) i due vertici della catena (o comunque di un'inferenza forte) è sicuramente da eliminare → in pratica è da eliminare quando è nella stessa riga/colonna/riquadro/cella dei due vertici della catena, ed ovviamente può essere in riga con un vertice e in riquadro con un altro etc.
- quando i due vertici della catena sono collegabili fra di loro con un'inferenza debole siamo in presenza di una catena circolare bidirezionale → in questo caso tutte le inferenze deboli della catena si possono considerare forti e si possono eliminare di conseguenza anche tutti i candidati che "vedono" i vertici di ogni inferenza debole (il caso più semplice e tipico è una "Alternating Inference Chain" tracciata su un "Naked Pair" ma ce ne sono di molto più complicate che portano ad eliminazioni assolutamente originali)
- Nelle affermazioni (o ipotesi) di candidati veri o falsi si
intende:
- blocco di candidati uguali in linea vero quando un candidato del blocco è vero (ovviamente non può essere vero più di uno)
- blocco di candidati uguali in linea falso quando nessun candidato del blocco è vero
- doppia coppia di candidati in due celle parte di "Almost Naked Pair" o "Almost Hidden Pair" vera quando entrambi i suoi candidati sono veri in una o l'altra delle sue celle
- doppia coppia di candidati in due celle parte di "Almost Naked Pair" o "Almost Hidden Pair" falsa quando uno solo dei due candidati è vero in una o l'altra delle sue celle (però uno dei due è sempre vero in una o l'altra cella altrimenti non potrebbe essere un "Almost Pair")
- coppia di candidati, in una cella con tre candidati totali, vera quando uno dei due candidati è vero
- coppia di candidati, in una cella con tre candidati totali, falsa quando nessuno dei due candidati è vero
"Alternating Inference Chains" è una tecnica logica che effettua delle eliminazioni assolutamente originali ed inoltre somma le possibilità di eliminazione di molte altre tecniche (vedi negli esempi grafici delle prossime pagine vari "Subsets" e "Fishes" rappresentati sotto forma di "Alternating Inference Chains").
Non risolve tutti gli schemi, per quello bisogna passare alle Forcing Chains e oltre, ma non sono molti quelli che "resistono".
Di seguito ci sono vari esempi di report grafico generati dal "Sudoku 9x9 Logic Solver & Report Builder" (vai al → DOWNLOAD) e molti altri si possono vedere nei files Excel con report di esempio scaricabili da questo sito.
Nelle pagine successive, gli esempi di report grafico sono così raggruppati:
- pagina 2: "Alternating Inference Chains" con vertici di singoli candidati o blocchi di candidati uguali;
- pagina 3: "Alternating Inference Chains" circolari bidirezionali ("Continous Nice Loop");
- pagina 4: "Alternating Inference Chains" con "Almost Naked Pair" e "Almost Hidden Pair" (prima parte);
- pagina 5: "Alternating Inference Chains" con "Almost Naked Pair" e "Almost Hidden Pair" (seconda parte);
- pagina 6: "Alternating Inference Chains" circolari e non che rappresentano dei "Fishes";
- pagina 7: "Alternating Inference Chains" tipo Subsets Loops (Naked Double Loops).
Clickando su ogni miniatura di schema Sudoku si passa, in un'altra finestra, ad un'ulteriore pagina con la stessa premessa sovrastante la miniatura, l'immagine ingrandita, l'analisi per ipotesi della catena ed eventuali altri commenti.
Per una migliore comprensione dei report grafici si può visionare la legenda in:
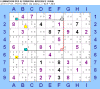
AIC con 2 strong links tipo "Skyscraper":
almeno un candidato fra i due
vertici ( 9 in A1 e 9 in B5 ) è vero
Possiamo eliminare:
il 9 in B2 perché in riquadro con il 9 in A1 e in colonna con il 9 in B5;
il 9 in A6 perché in riquadro con il 9 in B5 e in colonna con il 9 in A1.
Nella soluzione finale di questo schema sono veri tutti e due i vertici
della catena ( 9 in A1 e 9 in B5 ).